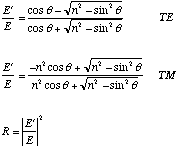The Opticon treatment of fissure-filling treatment emeralds with Opticon became an issue of huge controversy in the late 1990's. This article takes a close look at it and asks if Opticon is actually that different from fillers like cedarwood oil.
Emerald • Opticon Treatment • Cloak and Dagger
Get your facts first, and then you can distort them as much as you please. Mark Twain (as quoted by Kipling)
FOR THOSE NEW to the news, in the past few years, emerald traders have become the pariahs of our business, ranking right down there with terrorists, child pornographers and those who propose an increase in the minimum wage. If one reads the reports correctly, they tend to lurk in trench coats outside of playgrounds, ever ready to corrupt the morals of the nation's youth. Their weapon of choice: Opticon. By slipping a treated emerald from beneath their cloaks, they induce in their victims a permanent state of moral turpitude, leading them across to the dark side, a state of total and utter depravity.
Extreme rhetoric? Perhaps, but the mere mention of Opticon today seems to induce a type of collective hysteria that borders on paranoid schizophrenia. Just why is a mystery to this writer.

Figure 1 Due to the conditions under which they form, most emeralds contain numerous fractures and openings. This photo shows the classic three-phase inclusion of a Colombian emerald, consisting of a negative crystal filled with a gas bubble, a halite crystal and a brine solution. If cutting exposes this inclusion to the surface, it will fill with air, producing reflection. Such inclusions are typically filled with oil or resin to reduce the amount of reflection. (Photo: R.W. Hughes)
Let's get some facts. The stressful geologic conditions under which emerald forms means that virtually all natural emeralds contain numerous surface-reaching fractures and openings. Dealers reduce the visibility of these by filling them with a fluid. Traditionally, such fillers have been oils of various types, cedarwood oil being a common one; today, resins are also used. This type of enhancement process is one of the oldest in the business, with reports on it dating back over 600 years.

Figure 2 Another negative crystal in a Colombian emerald, this one containing more than one daughter crystal. (Photo: R.W. Hughes)
Just what is Opticon? It is a type of epoxy resin, and has been sold for decades. Indeed, it has been advertised as a fracture sealant in the Lapidary Journal since at least the early 1960s. What are some of the claims that have been made about Opticon? Some believe that, since Opticon is a type of epoxy, it is equivalent to gluing a stone together. The reality is far more mundane. Epoxy resins such as Opticon come in two parts – a resin and a hardener. Typically, for emerald treatment only the resin is used. The hardener, if used at all, is used solely to seal the surfaces. Thus Opticon is not used to "glue stones together."
But by far the strongest argument made by gemologists against Opticon is that it (and related resins) are so good at cloaking fractures that they disappear completely. The following is from the trial transcripts of the infamous Fred Ward emerald case:
In the case of oil, it's very efficient. It's been a traditional process. In the case of Opticon, it's about 30 to 40 percent more efficient than the oil. In other words, it mask [sic] the fractures much more completely than oil ever could.
Casper Beesley, June 19, 1997, testimony
Transcripts from Doree Waldbaum, et al VS. Blue Planet Gems, et al
Superior Court of the District of Columbia, Civil Division,
Civil Action Number: CA-5677–95
Masking refers to the ability of a filler to make a fracture invisible, and is a function of how closely the refractive index (RI) of the filler matches that of the gem being enhanced. The closer the RI's of the two substances, the better the masking. If the RI's are identical, no reflection will take place when light strikes the filled fracture, making it completely invisible.
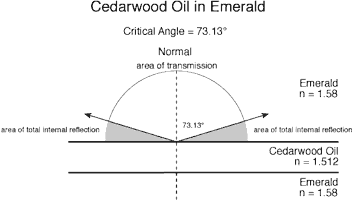
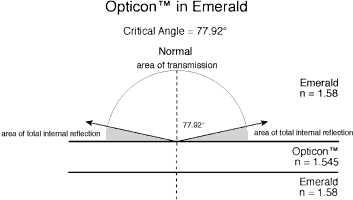
Figure 3 Cedarwood oil and Opticon in emerald. (Diagram © R.W. Hughes)
In an effort to separate fact from fancy, the author did a mathematical modeling of Opticon versus the traditional cedarwood oil (see the above illustration). Incredibly, this shows that, contrary to the above testimony, differences between the reflectivity of Opticon versus cedarwood oil are minor, on the order of 6–7%, far less than the 30–40% claimed. Suddenly, facts in hand, Opticon doesn't look so bad after all.
Emerald is among the most beautiful precious stones this planet has ever produced. It also tends to contain large numbers of surface-reaching fractures and openings. Thus the prevalence of clarity enhancements.

Figure 4 Filling fractures with a resin of similar RI to the host emerald typically produces a color flash effect. In this case, an orange flash is seen. (Photo: R.W. Hughes)

Figure 5 The same stone as above, but tilted slightly, so that the color flash is now blue. (Photo: R.W. Hughes)
The Luddites who pine for an enhancement-free world are merely guilty of flights of fancy. For that, they can be forgiven. Oh, my dearies, those days are gone. Long gone. You must let them go…
Unfortunately, it is far harder to forgive the self-appointed consumer advocates whose anti-Opticon vitriol and diatribes represent a de-facto crusade for the continuation of unstable enhancements like cedarwood oil. Today, those actions threaten to put a dagger through the very heart of the emerald business, an honorable trade which revolves around one of nature's most majestic creations. I simply cannot go along with it.

Note
Since publication, I have, with the most generous help of John Emmett and Karen Palmer of Crystal Chemistry (22721 NE 123rd Circle, Brush Prairie, WA 98606) refined the math to produce a more exact analysis of reflectivity from an oil-filled interface in emerald. The following table gives exact numbers. The emerald is assumed to have an RI of 1.58.
What this table clearly demonstrates is that filling a fissure or crack in an emerald with any of the commonly used fillers removes the lion's share of reflection when compared with air. Comparing the various fillers to one another reveals only slight differences in reflectivity.
|
Filler RI |
Critical |
Reflectance Percentages at Various Angles of Incidence |
|||||||||
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° | ||
| Air n = 1.000 |
39.27°
|
5.05
|
5.07
|
7.42
|
100
|
100
|
100
|
100
|
100
|
100
|
100
|
| n = 1.500 |
71.69°
|
0.07
|
0.07
|
0.07
|
0.08
|
0.11
|
0.25
|
1.05
|
17.01
|
100
|
100
|
| n = 1.517 |
73.77°
|
0.04
|
0.04
|
0.04
|
0.05
|
0.07
|
0.14
|
0.58
|
6.28
|
100
|
100
|
| n = 1.531 |
75.69°
|
0.02
|
0.02
|
0.03
|
0.03
|
0.04
|
0.08
|
0.32
|
2.82
|
100
|
100
|
| n = 1.550 |
78.82°
|
0.01
|
0.01
|
0.01
|
0.01
|
0.01
|
0.03
|
0.11
|
0.77
|
100
|
100
|
| n = 1.570 |
83.55°
|
0.00
|
0.00
|
0.00
|
0.00
|
0.00
|
0.00
|
0.01
|
0.07
|
1.73
|
100
|
|
John Emmett on Fissure Filling The following is John Emmett's explanation of the optics behind the above calculations. They make reference to an Excel spreadsheet which John and Karen created. Should you be interested in playing with this file, download it here. But be forewarned, neither John Emmett nor myself will be providing technical support for the use of this file. The Emmett tech-support hotline is already worn out on this problem and I, myself am mathematically challenged. All cracked up (with no place to go) To: Dick Hughes Subject: Your Problem (but not your only one) In this spreadsheet there are only four numbers you can enter: n1 in two places, and n2 in two places. The spreadsheet calculates the Relative Index of Refraction n = n2/n1, and the Critical Angle so don't try to enter these. From these numbers the spreadsheet calculates all of the reflectivities. Note you can change Emerald to any gemstone name you want, and likewise you can change the crack content to anything you want. Note that when you change the index of refraction of anything, the spreadsheet recalculates everything. In addition the reflectivity calculations are duplicated so you can directly compare an empty crack with a filled crack by seeing the numbers next to each other. Now for some explanations. The geometry, nomenclature, and equations used are presented in Grant R. Fowles' Introduction to Modern Optics (1968, Holt, Rinehart and Winston, New York). The geometry is shown in Figure 2.9, page 48 of this reference. The incident light ray is always in the region with the index of refraction n1, regardless of the relative index of refraction of the two materials. The reflected ray is always in region n1 also. The transmitted ray is always in the region with index n2. With these conventions, the spreadsheet always calculates the reflectivities correctly whether the incident ray is in the lower or higher refractive index region. Thus this spreadsheet is quite general, but you have to think carefully about what you are doing. The equations programmed into the spreadsheet are 2.58 and 2.59 on page 51 of the reference.
Where E'/E is the amplitude reflectivity of the electric field of the light, and R is the light intensity reflectivity. The Critical Angle is that angle where the reflectivity becomes 100%, and remains 100% for all larger angles. This occurs only for the situation where n<1.0. The equation for the critical angle is just:
Now what do TE and TM mean? As you know, there are two polarization directions of light which are perpendicular to each other and perpendicular to the direction of propagation of the light ray or beam. Unpolarized light can be described as equal amounts of the two polarizations. Because the reflectivities of interfaces are dependent on the polarization of the incident ray, we have to calculate it for each polarization. That is why the spreadsheet has two columns for the reflectivity. There are many ways to denote the two polarizations. This book has chosen TE (transverse electric) and TM (transverse magnetic). What does that mean? First, remember that the polarization direction and the electric field vector direction of light are the same thing. Second, transverse in this context means "perpendicular." Perpendicular to what? Perpendicular to the plane of incidence. This is an imaginary plane that contains both the incident and reflected ray. In my drawing Figure 1a, the plane of incidence is the sheet of paper. (Note: all my drawings are for the situation where n1>n2 which is why the transmitted ray bends the other way from the drawings in the book.) Note that in Figure 1a the little circles on the light rays are meant to denote the ends of the polarization direction arrows shown more clearly for the other polarization in Figure 1b. Now what does TM mean? Remember that light is made up of both an electric field and a magnetic field and that their vectors are mutually perpendicular to each other. So TM just means that the magnetic field vector is perpendicular to the Plane of Incidence. Since we normally think of polarization in terms of the electric vector direction, I have shown that as the arrows in the TM case in Figure 1b. Since light in most observational situations is made up of both polarizations we average the two single polarization reflectivities to calculate the real single surface reflectivity. Now on to the explanation of the problem I have calculated for you. As I understand your current interest, it is to calculate the reflectivity of a crack in a gemstone filled with anything like air, oil, Opticon, kangaroo piss, or whatever. Thus I have set up the problem in that way, i.e., the incident ray is in the gemstone (index n1) and is incident on the crack (index n2). This is shown in Figure 2. Now comes the subtle part. Note that there are really TWO reflections that count towards what you see; the reflection off the top of the crack AND the reflection off the bottom of the crack. Thus the reflectivity from the first two reflections of the crack is R + R(1–R)2, where R is the single surface reflectivity. For low reflectivities, this nearly DOUBLES the single surface reflectivity calculated in the spreadsheet! Don't forget this. Actually there are many more reflections but they contribute very little additional intensity (see figure 2). The enclosed spreadsheet has a lot of #NUM! entries courtesy of Excel. What is that all about? If you look at Equation 2.58 or 2.59 for the case where n<1.0, you can see that for some angles it is possible for the quantity under the square root sign to be negative. As you know, you can't take the square root of a negative number. Well actually you can, and the result is called a complex number because it contains two parts, a real part and an imaginary part denoted by the multiplier "i" which is equal to square root(-1). (I know you don't want to hear about this [your're right, I don't] but I must persist a little longer.) When you square a complex number to get to get the intensity reflectivity, you multiply the complex number (like a + ib) by its complex conjugate (which is a – ib). The result for the equations we are using is 1.0, that is the reflectivity is 100% for any complex number reflectivity. Now this simple Excel spreadsheet does not know about complex numbers, so when faced with taking the square root of a negative number it shouts HELP! (#NUM! in Excelspeak). So you know what to do, OK? Whenever you see #NUM! In the reflectivity column, just read it as 100%. Now notice another thing. The reflectivity changes relatively slowly with increasing angle until you near the critical angle where it increases very rapidly. Thus you go from a few tens of percent reflectivity to 100% in less than one degree! Positively magical! Now examine the reflectivity columns in the spreadsheet for the case where the indices of refraction of crack filler and emerald differ by only 0.02. Note that the normal incidence reflectivity is only .004%! If it is really this low, why can you see the crack at all? Its simple; either the surface is not emerald or it is not planar. Most cracks contain mineral alteration products or other impurities which have been deposited in the crack. Even boiling in acid does not fully remove these materials. These materials have a color contrast to the emerald which makes them more visible, or have indices of refraction which are different than emerald causing additional reflection. However, it is important to remember that even if it was totally an emerald surface, but that surface had a fine roughness, the oil, with its finite viscosity, might not completely wet the surface and thus not completely reduce the reflectivity. Another point I might make is that the closeness of the index match is not too important. Just use the spreadsheet to do an example or two for yourself. Thus the practice of filling tourmaline fractures with spermaceti (n=1.43) works quite well as most tourmaline fractures are very clean. I hope the foregoing answers your questions adequately. Sincerely, |
For more on the fracture filling of emerald, see this excellent article:
- Johnson, Mary L., Elen, Shane and Muhlmeister, Sam (1999) On the identification of various emerald filling substances. Gems & Gemology, Vol. 35, No. 2, Summer, pp. 82–107.
Author's Afterword
This article originally appeared in the GQ Eye (1998, Vol. 1, No. 1, Fall, p. 3, 6). For an updated take on this issue, see "The Digital Devil: Don't Forget to Flush."
About the Author
Richard W. Hughes is one of the world’s foremost experts on ruby and sapphire. The author of several books and over 170 articles, his writings and photographs have appeared in a diverse range of publications, and he has received numerous industry awards. Co-winner of the 2004 Edward J. Gübelin Most Valuable Article Award from Gems & Gemology magazine, the following year he was awarded a Richard T. Liddicoat Journalism Award from the American Gem Society. In 2010, he received the Antonio C. Bonanno Award for Excellence in Gemology from the Accredited Gemologists Association. The Association Française de Gemmologie (AFG) in 2013 named Richard as one of the fifty most important figures that have shaped the history of gems since antiquity. In 2016, Richard was awarded a visiting professorship at Shanghai's Tongji University. 2017 saw the publication of Richard's Ruby & Sapphire: A Gemologist's Guide, arguably the most complete book ever published on a single gem species and the culmination of nearly four decades of work in gemology.